Правильный шестиугольник и его свойства. Как нарисовать 6 угольник

Полезные советыПоложительные шестиугольники очень популярны в природе. Например, весь улей медоносной пчелы представляет собой положительный шестиугольник. Кроме того, кристаллическая решетка графена (модификация углерода) также имеет форму положительного шестиугольника.

Построение правильного шестигранника

Определение и построение положительного шестиугольника. Периметр, площадь, окружность и радиус эндоцикла. Интересные структуры и шестиугольные поверхности.

• Если при использовании метода с циркулем вы соединили каждую отметку вместо всех шести, то получите равносторонний треугольник.
• Карандаш и циркуль должны быть острыми, чтобы минимизировать ошибки от слишком широких отметок.
• Не давите слишком сильно на карандаш или циркуль при рисовании шестиугольника, с тем чтобы у вас была возможность стереть лишние линии.
• Чтобы измерения были точными, измерьте углы шестиугольника.

Определение и построение

Правильный шестиугольник — это плоская фигура с шестью сторонами равной длины и равными углами.

Если вы помните формулу для суммы углов многоугольника

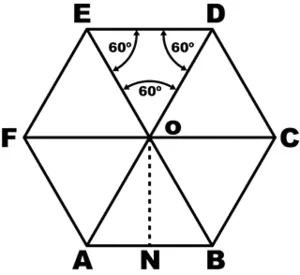
720° на этой диаграмме, мы видим, что угол равен 720°. Поскольку все углы на диаграмме равны, легко вычислить, что каждый из них равен 120°.

Нарисовать шестиугольник очень просто. Все, что вам нужно, — это компас и линейка.

Далее следуют пошаговые инструкции.

1. чертится прямая линия и на ней ставится точка;
2. из этой точки строится окружность (она является ее центром);
3. из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
4. после этого отрезками последовательно соединяются все точки на первой окружности.

При необходимости вы можете сделать это без линий, нарисовав пять окружностей одинакового радиуса.

Полученная форма будет правильным шестиугольником. Это показано ниже.

Шестиугольник, выпуклый и невыпуклый шестиугольник:

Шестиугольник — это многоугольник с шестью углами.

Шестиугольник — это многоугольник, общее число углов (вершин) которого равно шести.

Шестиугольник может быть выпуклым или невыпуклым.

Выпуклый многоугольник — это многоугольник, все точки которого находятся по одну сторону от прямой, проходящей через две соседние вершины. Все остальные многоугольники являются невыпуклыми.

Аналогично, выпуклый шестиугольник — это шестиугольник, все точки которого лежат по одну сторону от прямой, проходящей через две соседние вершины.

Рисунок 1. Выпуклый шестиугольник

Рисунок 2. Невыпуклый шестиугольник

Сумма внутренних углов каждого выпуклого шестиугольника равна 720°.

7. нарисуйте положительный шестиугольник. Разместите шесть точек из предыдущего шага попарно. Начертите секции карандашом и линейкой. Конечным результатом будет правильный шестиугольник. После завершения строительства вспомогательные элементы (арки и круги) разрешается удалять.

Правильный шестиугольник и его свойства

Тема многоугольников изучается в школьной программе, но ей уделяется недостаточно внимания. Между тем, интересно отметить, что построение шестиугольника — это не просто построение шестиугольника. Это особенно актуально для обычных шестиугольников или шестиугольников. Это происходит потому, что в этой форме находится множество физических объектов. К ним относятся соты. Эта форма очень часто используется на практике.

Правильный шестиугольник — это плоская фигура с шестью сторонами равной длины и равными углами.

Если вы помните формулу для суммы углов многоугольника

720° на этой диаграмме, мы видим, что угол равен 720°. Поскольку все углы на диаграмме равны, легко вычислить, что каждый из них равен 120°.

Нарисовать шестиугольник очень просто. Все, что вам нужно, — это компас и линейка.

Далее следуют пошаговые инструкции.

1. чертится прямая линия и на ней ставится точка;
2. из этой точки строится окружность (она является ее центром);
3. из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
4. после этого отрезками последовательно соединяются все точки на первой окружности.

При необходимости вы можете сделать это без линий, нарисовав пять окружностей одинакового радиуса.

Полученная форма будет правильным шестиугольником. Это показано ниже.

Свойства простые и интересные

Чтобы понять свойства правильного шестиугольника, имеет смысл разделить его на шесть треугольников.

Это помогает дополнительно объяснить его свойства. Основные из них следующие.

1. диаметр описанной окружности;
2. диаметр вписанной окружности;
3. площадь;
4. периметр.

Описанная окружность и возможность построения

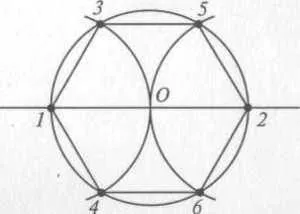
Вы можете нарисовать круг вокруг шестиугольника, но только один. Эта форма является нормальной и может быть простой. Биссектрисы можно провести из двух смежных углов. Они пересекаются в точке O и образуют треугольник со стороной между ними.

Углы между сторонами шестиугольника и бистензора составляют по 60°, поэтому можно сказать, что треугольник aob действительно является изошиной. Третий угол также эквивалентен, так как равен 60°. Поскольку отрезки OA и OB равны, они, по-видимому, могут действовать как радиусы цикла.

Затем мы можем перейти на следующую сторону и откусить от угла до точки C. Вы получаете еще один равносторонний треугольник, сторона АВ общая для обоих, а ОС — еще один луч, через который он циклически проходит. Существует шесть таких треугольников с общей вершиной в точке O. Можно описать круг, и только один, радиус которого равен стороне шестиугольника.

Поэтому эту фигуру можно построить с помощью компаса и линейки.

Затем область этого цикла становится нормальной:.

Вписанная окружность

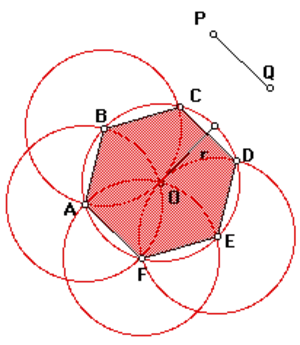
Центр периметра совпадает с центром в ячейке. Чтобы проверить это, можно нарисовать шестиугольники перпендикулярно боковым сценам. Это высоты треугольников, из которых состоит шестиугольник. Кроме того, в треугольниках изошелла высота является медианой по отношению к стороне, на которой она расположена. Поэтому высота — это только срединная вертикаль, которая является радиусом регистрационного цикла.

Высота равностороннего треугольника вычисляется просто

h² = a²-(a/2)² = a²3/4, h = a(√3)2

так как r = a и r = h.

Таким образом, зарегистрированная окружность проходит через центр стороны нормального шестиугольника.

Его диапазон — да.

То есть, три четверти региона.

Периметр и площадь

Граница ясна: она равна сумме длин сторон.

p = 6a или p = 6r

Однако площадь — это сумма всех шести треугольников, на которые можно разделить шестиугольник. Площадь треугольника вычисляется как половина основания высоты, таким образом

s = 6(a/2)(a(√3)/2) = 6a²(√3)/4 = 3a²(√3)/2 или

Желающие могут вычислить эту площадь через радиус Акоккаля.

Занимательные построения

Шестиугольные треугольники могут быть записаны с помощью треугольников на сторонах, соединяющихся через вершины один за другим.

Всего их два, и их запрос дает «Звезду Давида». Каждый из этих треугольников является равносторонним треугольником. Это несложно понять. Если посмотреть на сторону AC, то она принадлежит двум треугольникам, BAC и AEC. Если в начале их ab = bc и угол между ними равен 120°, то остальные по 30°. Из этого можно сделать логические выводы.

От теории к практике

Свойства шестиугольников преимущественно используются как в природе, так и в различных областях человеческой деятельности. В первую очередь это относится к винтам и гайкам — первый и второй уровни представляют собой обычные шестиугольники, если не учитывать кантотомию. Размер ключа соответствует диаметру регистрационного цикла, т.е. расстоянию между противоположными сторонами.

Шестиугольные плитки также нашли свое применение. Они встречаются гораздо реже, чем четырехсторонние плитки, но их легче размещать; три плитки встречаются в одной точке, а не четыре. Композиция оказывается очень интересной:…

Бетонную плитку можно также использовать для мощения.

Преобладание шестиугольников в природе легко объяснимо. Поэтому круги и сферы легче крепить плотно друг к другу, если они имеют одинаковый диаметр. Именно поэтому соты медоносных пчел имеют такую форму.

Как только вы освоите этот объект, вам будет легче визуализировать различные объекты на его основе в будущем. В частности, нет проблем с различными коробками, упаковками, приборами, зданиями и т.д.

Совет 2: Как верно строить шестиугольник

Шестиугольник — это многоугольник с шестью углами и шестью сторонами. Многоугольники могут быть как выпуклыми, так и вогнутыми. Все внутренние углы выпуклого шестиугольника тупые. Вогнутый шестиугольник имеет один или несколько острых углов. Шестиугольники очень легко создавать. Это делается в несколько этапов.

Вам понадобятся.

Инструкция

1. возьмите лист бумаги и отметьте на нем шесть точек, как показано на рисунке 1.

2. после того, как вы отметили точки, возьмите линейку и карандаш и соедините точки одну за другой с помощью, как показано на рисунке 2.

Видео по теме.

Блокнот! Сумма всех внутренних углов шестиугольника равна 720°.

Совет 3: Как начертить шестиугольник

Шестиугольник — это многоугольник с шестью углами. Чтобы нарисовать любой шестиугольник, необходимо выполнить каждые два действия.

Вам понадобятся.

Для любого числа n, начиная с n = 3, можно построить регулярный n-гон. На следующей диаграмме показаны примеры таких n-угольников.

Инструкция

1. возьмите карандаш и отметьте шесть точек на странице. Эти точки служат углами шестиугольника. (рис. 1).

2.Возьмите линейку и проведите шесть прямых отрезков, используя определенные точки. Эти участки должны быть соединены между собой в ранее нанесенных точках (рис. 2).

Видео по теме.

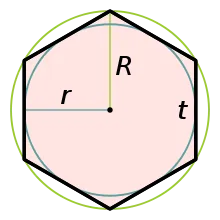
Обратите внимание. Особый тип шестиугольника — положительный шестиугольник. Они названы так потому, что все стороны и углы равны. Вы можете нарисовать или вырезать круги вокруг таких шестиугольников. Стоит отметить, что стороны положительного шестиугольника уменьшаются вдвое в точке, образованной контактом между конечной окружностью и сторонами шестиугольника.

Полезные советыПоложительные шестиугольники очень популярны в природе. Например, весь улей медоносной пчелы представляет собой положительный шестиугольник. Кроме того, кристаллическая решетка графена (модификация углерода) также имеет форму положительного шестиугольника.

То, как устроен любой из углов, является главным вопросом. Однако под некоторыми углами задача незаметно упрощается. Один из таких углов составляет 30 градусов. Это? / равно 6, т.е. 30 является делителем 180. Кроме того, его синус является синусом квадрата. Это помогает в его строительстве.

Вам понадобятся.

Инструкция

1. сначала посмотрите на очень примитивную среду с угловым транспортиром под рукой. Затем вы можете легко провести линию, образующую угол 30° с данной линией, с ее опорой.

2. в дополнение к транспортиру есть угольники, один из которых соответствует 30 градусам. Тогда другой угол транспортира равен 60 градусам. Это означает, что для проведения требуемой линии необходимы визуально меньшие углы.

3. теперь перейдем к важному способу создания угла в 30 градусов. Как вы знаете, полутон угла 30° равен 1/2. Чтобы построить его, необходимо установить правильный угол. Можно поднять две вертикальные линии. Однако отношение между вертикальными линиями можно вычислить только приблизительно (только если у вас нет калькулятора), так как касательная линия 30° является неявным числом. Таким образом, можно установить угол приблизительно в 30 градусов.

4. в этом случае вы также можете составить точный план. Постройте две перпендикулярные прямые, на которых расположены прямые углы треугольника. Используйте опорный компас (угол b-прямой), чтобы обеспечить удаление некоторой длины катетера BC по прямой линии. Затем увеличьте длину между ножками компаса в два раза. Это элементарно. Найдите точку пересечения окружности с другой прямой линией с лучом в точке C. Эта точка находится под углом A 30 градусов к точке A прямоугольного треугольника ABC.

5.? Применив равенство /6, вы получите угол в 30 градусов в окружности. Сформируйте круг с радиусом ob. Пусть oa = ob = r — радиус окружности ob = r. где угол = 30 градусов. Предположим, что OE — это высота треугольника изошеллы, ее деление и медиана. Тогда, согласно виду угла aoE = 15 градусов, а половинный угол sin(15o) = (sqrt(3)-1)/(2*sqrt(2)). Следовательно, ae = r*sin(15). Следовательно, ab = 2AE = 2r*sin(15o). Постройте цикл радиуса BA в центре B и найдите точку пересечения этого цикла с начальной точкой. Угол AOB будет равен 30o.

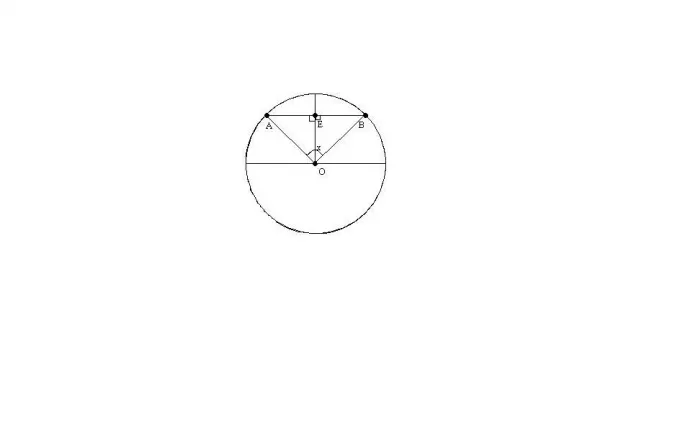
6. если длина дуги может быть определена каким-либо способом, то при откладывании дуги вы также получите угол 30°;*r/6.

ВНИМАНИЕ! Помните, что приблизить можно только угол пункта 5, так как в вычислениях присутствуют иррациональные числа.

Шестиугольники являются частным случаем многоугольников — это фигуры, образованные большинством точек уровня, которые являются касательными к замкнутому многоугольнику. Положительные шестиугольники (гексагоны) также являются особым случаем. Это многоугольник с шестью равными сторонами и равными углами. Эта фигура важна тем, что длины всех сторон равны радиусу окружности, описанной вокруг фигуры.

Вам понадобятся.

Инструкция

1. выберите длину стороны шестигранника. Возьмите компас и установите расстояние между концом иглы на одной из ножек и ведущим концом на другой ножке равным длине стороны проектируемой фигуры. Если эта точка не является критической, можно использовать линейку или выбрать случайное расстояние. Если возможно, закрепите круглые ножки винтами.

2. нарисовать цикл компаса. Выбранное расстояние между ножками является радиусом круга.

3. разделите окружность на шесть равных частей точками. Эти точки являются угловыми вершинами шестиугольника и, следовательно, концами частей, представляющих его стороны.

4. установите компасную лапку с иглой в любом месте очерченной линии окружности. Игла должна правильно проникнуть в линию. Точность плана напрямую зависит от точности окружности. Начертите дугу с помощью компаса так, чтобы окружность сначала пересеклась в двух указанных точках.

5. с помощью иглы переместите ножку компаса на одно из пересечений дуги, спроектированной в исходном цикле. Также натяните еще один лук. Это также пересекает окружность в двух точках (одна из которых совпадает с точкой в предыдущем положении круговой иглы).

6. Аналогично вставьте круглую иглу и вытяните бантик еще четыре раза. Двигайте иглу по кругу в одном и том же направлении (всегда по часовой стрелке или против часовой стрелки). В результате между дугой и исходным циклом должно быть найдено шесть пересечений.

7. нарисуйте положительный шестиугольник. Разместите шесть точек из предыдущего шага попарно. Начертите секции карандашом и линейкой. Конечным результатом будет правильный шестиугольник. После завершения строительства вспомогательные элементы (арки и круги) разрешается удалять.

Примечание: целесообразно выбирать расстояние между ножками компаса таким образом, чтобы угол между ними составлял 15-30 градусов. В противном случае это расстояние можно легко перепутать при внедрении структуры.

При строительстве или разработке дизайна дома угол часто должен быть равен узкому существующему дизайну. На ум приходят модели и поддержка школьных геометрических навыков.